FLUIDS AT NANOSCALES

At macroscopic scales the flow velocity of fluids is assumed to equal that of an adjacent solid at their interface. This boundary condition leads to singular stresses and energy dissipation in two simple geometries. The first is contact line motion, where the interface between two fluids advances over a solid at velocity U. The second is cavity flow, where the top of a cavity moves at velocity U while the other walls remain stationary. In both cases the velocity must change from U to 0 over a distance that vanishes at the corner where two interfaces intersect. This leads to a logarithmic divergence in the total force and dissipation.

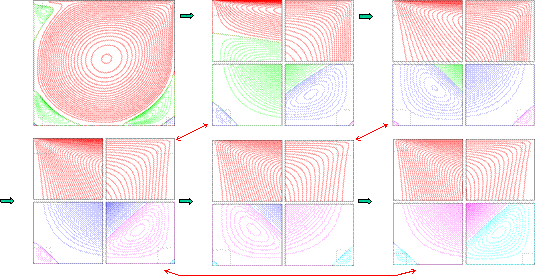
We developed a multiscale approach that uses a continuum mechanics description except near the singular corners. There, discrete atoms are followed. The method allows particles and heat to flow between continuum and atomistic regions. In the plots below the corners are magnified by increasing factors from 2³ to 2¹¹. The stress is resolved over 6 orders of magnitude in length from ~nm to ~mm. The region within ~12 atoms from the corners carries 20 to 30% of the total force.

At atomic scales deviations from the no-slip boundary condition are observed. Our studies revealed that these deviations can become extreme for fluid mixtures. Large jumps in velocity arise from gradients in interfacial energy or concentration. A movie showing how this can be used to drive a nanometer is at movies.html.